misteri su cui meditare
La sequenza di Fibonacci, una serie di numeri che ha affascinato matematici, scienziati e artisti, ha una ricca storia che risale all'antica civiltà indiana. Sebbene prenda il nome dal matematico italiano Leonardo di Pisa, noto come Fibonacci, le origini della sequenza sono profondamente radicate nelle tradizioni intellettuali dell'antica India. Questo articolo esplora il contesto storico della sequenza di Fibonacci, i contributi significativi dei matematici indiani e il suo impatto duraturo.
Sequenza di Fibonacci: una panoramica storica
La sequenza di Fibonacci inizia con 0 e 1, e ogni numero successivo è la somma dei due precedenti. Questa sequenza semplice ma profonda appare in vari aspetti della natura, dell'arte e della scienza. Introdotta nel mondo occidentale da Fibonacci nel suo libro “Liber Abaci” (1202), la sequenza era stata studiata dagli studiosi indiani molto prima del suo tempo.
I matematici dell'antica India e i loro contributi
Pingala e le prime menzioni della sequenza
Uno dei primi riferimenti alla sequenza di Fibonacci si trova nelle opere di Pingala, un antico studioso indiano vissuto intorno al II secolo a.C. Nel suo trattato sulla prosodia sanscrita, Pingala descrisse una sequenza simile ai numeri di Fibonacci nel contesto della metrica poetica. Questo lavoro fondamentale gettò le basi per i successivi sviluppi matematici.
Le espansioni di Virahanka, Gopāla e Hemachandra
Secoli dopo Pingala, matematici come Virahanka, Gopāla e Hemachandra ampliarono il suo lavoro. Nel VI secolo d.C., Virahanka contribuì alla comprensione della sequenza, mentre Hemachandra nel XII secolo d.C. fornì una chiara articolazione della sequenza che conosciamo oggi. Questi studiosi applicarono la sequenza per risolvere problemi di prosodia sanscrita, dimostrandone le applicazioni pratiche nella poesia.
La sequenza di Fibonacci nella prosodia sanscrita
Il ruolo della poesia sanscrita nello sviluppo matematico
La prosodia sanscrita, lo studio dei metri poetici, ha svolto un ruolo cruciale nello sviluppo dei concetti matematici nell'antica India. I modelli di sillabe lunghe (guru) e brevi (laghu) nei metri poetici rispecchiavano la sequenza di Fibonacci, mettendo in evidenza la profonda connessione tra lingua e matematica.
La prosodia si riferisce agli schemi di ritmo e suono utilizzati nella poesia. Nella prosodia sanscrita, gli schemi di sillabe lunghe e brevi erano utilizzati per strutturare i versi. Ad esempio, una sillaba lunga (guru) poteva essere rappresentata dal numero 2 e una sillaba breve (laghu) dal numero 1. Questi schemi aiutavano i poeti a mantenere una struttura ritmica.
Spiegazione del piede metrico e del modello metrico:
Piede metrico: in poesia, un piede metrico è un'unità di misura di base dei modelli sillabici. Ogni piede è costituito da una combinazione di sillabe accentate e non accentate. Ad esempio, un giambico (un tipo di piede metrico) è costituito da una sillaba non accentata seguita da una sillaba accentata (ad esempio, “da-DUM”).
Schema metrico: si riferisce alla disposizione dei piedi metrici in un verso di poesia. Diversi tipi di schemi metrici vengono utilizzati per creare vari effetti ritmici.
Esempi nella poesia inglese:
Pentametro giambico: questo metro comune nella poesia inglese consiste di cinque giambi per verso (un giambo è un piede metrico con una sillaba breve seguita da una sillaba lunga). Un esempio tratto da Shakespeare:
“Posso paragonarti a un giorno d'estate?”
Qui, ogni verso ha dieci sillabe in uno schema di sillabe atone/tone.
Esametro dattilico: questo metro è spesso utilizzato nella poesia epica, come nell'Iliade di Omero:
“Canta, o dea, l'ira di Achille, figlio di Peleo”
Ogni verso è composto da sei piedi, dove un piede può essere una combinazione di sillabe lunghe e brevi.
Nella prosodia sanscrita, modelli simili erano usati per strutturare i versi, ma i modelli e le regole specifici erano diversi e spesso più complessi. L'approccio matematico a questi modelli aiutò gli antichi matematici indiani a sviluppare una comprensione più profonda delle sequenze e delle serie, che alla fine si collegarono alla sequenza di Fibonacci.
Mātrāmeru: il collegamento sanscrito
L'opera di Pingala includeva il concetto di mātrāmeru, simile alla sequenza di Fibonacci. Il termine “mātrāmeru” può essere scomposto in ‘mātrā’ (sillaba) e “meru” (montagna), riferendosi metaforicamente a una montagna di sillabe. Nel contesto della prosodia, rappresenta la disposizione di sillabe lunghe e brevi per formare metri poetici.
Esempio in sanscrito (con traslitterazione):
Nello studio del Chandas Shastra (scienza dei metri) di Pingala, il seguente esempio illustra l'uso del mātrāmeru:
छन्दः शास्त्र (Chandas Shastra)
Una sequenza tipica potrebbe apparire così in sanscrito:
ल (laghu) ग (guru) लल (laghu-guru-laghu)
Traslitterazione:
La (breve) Ga (lunga) Lala (breve-lunga-breve)
La sequenza segue lo schema in cui ogni “laghu” (1) e “guru” (2) si sommano per formare il modello metrico successivo, in modo simile a come vengono generati i numeri di Fibonacci.
Influenza globale dei contributi indiani
L'introduzione di Fibonacci in Occidente
I viaggi di Fibonacci nel Mediterraneo orientale e nel Nord Africa lo hanno esposto alle conoscenze matematiche degli studiosi arabi e indiani. Al suo ritorno a Pisa, pubblicò il “Liber Abaci”, introducendo la sequenza in Europa. Sebbene Fibonacci non abbia esplicitamente citato i matematici indiani, la loro influenza è evidente nel suo lavoro.
Riconoscimento moderno e idee sbagliate
Oggi, la sequenza di Fibonacci è celebrata per le sue applicazioni in vari campi, dalla biologia all'informatica. Tuttavia, persistono idee errate sulle sue origini, che spesso trascurano i contributi significativi degli studiosi indiani. Riconoscere questi primi contributi arricchisce la nostra comprensione della storia della sequenza.
Il significato e le applicazioni della sequenza di Fibonacci
Applicazioni matematiche e scientifiche
La sequenza di Fibonacci ha numerose applicazioni in matematica e scienze. Appare nei modelli di ramificazione degli alberi, nella disposizione delle foglie su uno stelo e nei modelli riproduttivi di vari organismi. In matematica, la sequenza è strettamente correlata al rapporto aureo, un altro concetto che ha affascinato gli studiosi per secoli.
Influenza culturale ed estetica
Al di là del suo significato scientifico, la sequenza di Fibonacci ha influenzato l'arte, la musica e l'architettura. Il rapporto aureo, derivato dalla sequenza, è spesso associato alla perfezione estetica. Artisti e architetti hanno utilizzato questo rapporto per creare composizioni visivamente piacevoli, dal Partenone nell'antica Grecia alle opere d'arte moderne.
La sequenza di Fibonacci oggi
La sequenza di Fibonacci è una serie di numeri in cui ogni numero è la somma dei due precedenti, a partire da 0 e 1. In termini matematici, si presenta così: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34 e così via. Ogni numero è generato sommando i due numeri che lo precedono.
Questa sequenza appare in molti fenomeni naturali, come i modelli di ramificazione degli alberi, la disposizione delle foglie su uno stelo, la fioritura di un carciofo, la disposizione di una pigna e l'albero genealogico delle api mellifere.

Oltre alla sua presenza in natura, la sequenza di Fibonacci è utilizzata negli algoritmi informatici, nei mercati finanziari per prevedere i movimenti delle azioni e in vari campi dell'arte e dell'architettura per creare disegni visivamente accattivanti basati sul rapporto aureo, che è strettamente correlato alla sequenza.
Ad esempio, nella disposizione delle foglie su uno stelo di una pianta, ogni foglia è posizionata con un angolo che si avvicina al rapporto aureo, consentendo un'esposizione ottimale alla luce e un'efficienza dello spazio. Questa presenza naturale della sequenza di Fibonacci illustra quanto questo principio matematico sia fondamentale e diffuso sia in natura che nelle strutture create dall'uomo.
Il rapporto aureo e i riferimenti nell'antica India
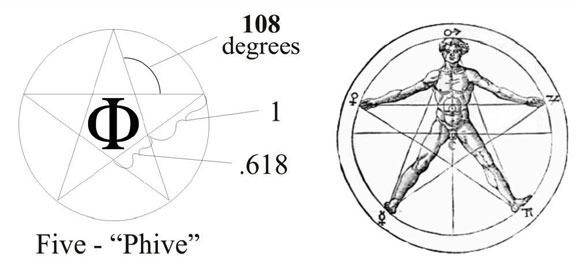
Il rapporto aureo, pari a circa 1,618, è un principio matematico secondo cui il rapporto tra un tutto e la sua parte maggiore è uguale al rapporto tra la parte maggiore e la parte minore. Questo rapporto, noto per il suo fascino estetico, appare in natura, nell'arte e nell'architettura.
Sebbene il rapporto aureo sia spesso associato a matematici greci come Euclide, anche gli antichi studiosi indiani dimostrarono di comprendere i principi geometrici correlati. Bhaskara II, un matematico indiano del XII secolo, descrisse nella sua opera “Lilavati” alcune costruzioni geometriche in linea con il rapporto aureo, in particolare nella costruzione di un pentagono.
Sebbene non abbia menzionato esplicitamente il rapporto aureo, le relazioni geometriche di cui ha discusso sono strettamente correlate ad esso.
Inoltre, la sequenza di Fibonacci, che si avvicina al rapporto aureo, è stata utilizzata nell'antica prosodia indiana da studiosi come Pingala. La presenza della sequenza nella poesia sanscrita indica una comprensione implicita dei principi alla base del rapporto aureo.
Pertanto, sebbene non sia esplicitamente documentato, i principi estetici e matematici del rapporto aureo erano apprezzati e applicati in vari contesti nell'antica India.
Fenomeni naturali
Loto indiano (Nelumbo nucifera):
Il loto sacro, molto diffuso in India, ha spesso 8, 13 o 21 petali, tutti numeri di Fibonacci. Anche la disposizione dei suoi semi segue un modello a spirale correlato al rapporto aureo.
Albero di banyan (Ficus benghalensis):
L'albero nazionale dell'India presenta modelli di Fibonacci nella sua struttura ramificata. Man mano che l'albero cresce, le sue radici aeree formano nuovi tronchi, creando una rete complessa che segue modelli di crescita simili a quelli di Fibonacci.
Pavone (Pavo cristatus):
L'uccello nazionale dell'India presenta spirali di Fibonacci nella disposizione delle sue penne della coda. Le macchie oculari sulle penne sono spesso disposte in spirali che si avvicinano al rapporto aureo.
Pigne indiane:
Le pigne che si trovano nelle regioni himalayane dell'India, come quelle del pino Chir (Pinus roxburghii), presentano modelli a spirale che seguono la sequenza di Fibonacci.
Tigre del Bengala (Panthera tigris):
Le strisce della tigre del Bengala, pur non seguendo rigorosamente la sequenza di Fibonacci, spesso presentano modelli che si avvicinano al rapporto aureo nella loro spaziatura e disposizione.
Strutture artificiali
Taj Mahal, Agra:
Sebbene non sia stato progettato esplicitamente utilizzando la sequenza di Fibonacci, le proporzioni del Taj Mahal sono strettamente allineate al rapporto aureo. Si dice che l'altezza della cupola principale rispetto alla larghezza e la disposizione dei giardini si avvicinino a questo rapporto.
Tempio del Sole di Konark, Odisha:
Questo tempio del XIII secolo è progettato come un enorme carro con 12 coppie di ruote. Si dice che i rapporti tra i vari elementi della struttura, comprese le ruote e il corpo del tempio, si avvicinino al rapporto aureo.
Tempio di Meenakshi, Madurai:
Gli intricati gopuram (torri d'ingresso) di questo complesso templare presentano motivi frattali nella loro architettura, che si riferiscono a modelli di crescita simili a quelli di Fibonacci.
Jantar Mantar, Jaipur:
Sebbene sia principalmente un osservatorio astronomico, alcuni degli strumenti di questo complesso del XVIII secolo, come il Samrat Yantra (meridiana), incorporano proporzioni che si avvicinano molto al rapporto aureo.
Chand Baori Stepwell, Rajasthan:
Questo antico pozzo a gradini ha 3.500 gradini stretti disposti in perfetta simmetria. Il motivo ripetitivo e le proporzioni dei gradini e dei livelli ricordano le sequenze di Fibonacci.
Questi esempi dimostrano come la sequenza di Fibonacci e il rapporto aureo non siano solo concetti matematici, ma siano profondamente radicati sia nel mondo naturale che nel patrimonio culturale dell'India.
Domande frequenti
Chi ha scoperto per primo la sequenza di Fibonacci?
R: Sebbene la sequenza prenda il nome da Leonardo di Pisa (Fibonacci), in realtà era già stata studiata dagli antichi matematici indiani molto tempo prima. Pingala, uno studioso indiano del II secolo a.C. circa, è considerato uno dei primi a fare riferimento a una sequenza simile nella sua opera sulla prosodia sanscrita.
In che modo la sequenza di Fibonacci è collegata alla poesia sanscrita?
R: La sequenza di Fibonacci era utilizzata nella prosodia sanscrita per strutturare i metri poetici. Antichi studiosi indiani come Pingala, Virahanka e Hemachandra applicarono la sequenza ai modelli di sillabe lunghe (guru) e brevi (laghu) nella poesia, dimostrando un'applicazione pratica del concetto matematico.
Che cos'è il concetto di mātrāmeru?
R: Mātrāmeru è un concetto introdotto da Pingala simile alla sequenza di Fibonacci. Si riferisce alla disposizione delle sillabe lunghe e brevi nei metri poetici, metaforicamente descritta come una “montagna di sillabe”.
Come è arrivata la sequenza di Fibonacci nel mondo occidentale?
R: Leonardo di Pisa (Fibonacci) introdusse la sequenza in Europa attraverso il suo libro “Liber Abaci” nel 1202. Probabilmente ne venne a conoscenza durante i suoi viaggi nel Mediterraneo orientale e nel Nord Africa, dove entrò in contatto con le conoscenze matematiche arabe e indiane.
Quali sono alcune applicazioni moderne della sequenza di Fibonacci?
R: La sequenza di Fibonacci trova applicazione in vari campi, tra cui:
Biologia (ad esempio, modelli di ramificazione degli alberi, modelli riproduttivi degli organismi)
Informatica (analisi e progettazione di algoritmi)
Mercati finanziari (strumento di analisi tecnica)
Arte e architettura (composizioni estetiche basate sul rapporto aureo)
Teoria musicale (ritmi e progressioni di accordi)
In che modo la sequenza di Fibonacci è correlata al rapporto aureo?
R: Man mano che la sequenza di Fibonacci progredisce, il rapporto tra i termini successivi converge verso il rapporto aureo (circa 1,618). Questa connessione collega la sequenza ai concetti di bellezza estetica nell'arte e nella natura.
Perché è importante riconoscere le origini indiane della sequenza di Fibonacci?
R: Riconoscere le origini indiane della sequenza di Fibonacci fornisce una prospettiva storica più accurata, riconosce i contributi degli antichi matematici indiani e arricchisce la nostra comprensione dello sviluppo globale dei concetti matematici.
Che cos'è e perché è importante?
La sequenza di Fibonacci è una serie di numeri in cui ogni numero è la somma dei due precedenti. In genere inizia con 0 e 1 e continua all'infinito. La sequenza è la seguente: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ... Matematicamente, può essere espressa come: F(n) = F(n-1) + F(n-2) Dove F(n) è l'ennesimo termine della sequenza. Il significato della sequenza di Fibonacci va ben oltre la sua semplice definizione matematica:
Rapporto aureo: man mano che la sequenza procede, il rapporto tra i termini successivi converge verso il rapporto aureo (circa 1,618033988749895), un numero con proprietà matematiche uniche e un fascino estetico.
Fenomeni naturali: la sequenza appare frequentemente in natura, dalla disposizione delle foglie sugli steli ai motivi a spirale nelle pigne, nei girasoli e nelle galassie.
Applicazioni biologiche: modella la riproduzione dei conigli in condizioni ideali e descrive la ramificazione degli alberi e la disposizione delle foglie su alcune piante.
Arte e architettura: il rapporto aureo derivato dalla sequenza di Fibonacci è stato utilizzato nell'arte e nell'architettura per le sue proprietà estetiche, dalle antiche strutture greche al design moderno.
Mercati finanziari: alcuni trader utilizzano i ritracciamenti di Fibonacci, basati sui numeri chiave della sequenza, come strumento di analisi tecnica.
Informatica: la sequenza è spesso utilizzata nell'analisi e nella progettazione di algoritmi, in particolare nei problemi di ottimizzazione e negli algoritmi ricorsivi.
Teoria musicale: alcuni compositori hanno utilizzato la sequenza per determinare ritmi, progressioni di accordi e persino la struttura di interi brani.
Ottimizzazione: nell'informatica e nella matematica, la sequenza di Fibonacci è utilizzata per analizzare e ottimizzare alcuni tipi di algoritmi.
Teoria dei numeri: la sequenza ha numerose proprietà matematiche interessanti che la rendono oggetto di studio nella teoria dei numeri.
Strumento di risoluzione dei problemi: la sua natura ricorsiva la rende un eccellente esempio introduttivo per insegnare il pensiero ricorsivo e la programmazione.
Le ampie applicazioni della sequenza di Fibonacci e la sua frequente presenza in natura hanno portato molti a considerarla un modello fondamentale nell'universo. Anche se questa potrebbe essere un'esagerazione, le sue proprietà matematiche e le sue applicazioni pratiche la rendono un concetto affascinante e importante in vari campi di studio.
Conclusione
La sequenza di Fibonacci è una testimonianza dell'atemporalità e dell'universalità delle idee matematiche. Sebbene porti il nome di un matematico italiano, le sue radici affondano profondamente nelle tradizioni intellettuali dell'antica India. Esplorando i contributi degli studiosi indiani, acquisiamo una comprensione più ricca della storia della sequenza e del suo impatto duraturo in vari campi.







